1.1.1 Grundstrukturen mit einer Verknüpfung

Sei $G$ Menge mit einer Verknüpfung

$$\circ: G \times G \rightarrow G, (f,g) \mapsto f\circ g$$

(kurz geschrieben: $fg:=f\circ g$ ).

1. G heißt Halbgruppe, falls die Verknüpfung assoziativ ist, d.h.
   $$\forall f,g,h \in G: f(gh)=(fg)h$$

2. G heißt Monoid, falls G eine Halbgruppe ist mit neutralem Element, d.h.
   $$\exists e \in G: eg=ge=g$$

3. G heißt Gruppe, falls G ein Monoid ist und jedes Element ein inverses Element besitzt, d.h.
   $$\forall g\in G \exists g^{-1}\in G: g^{-1}g=gg^{-1}=e$$

4. G ist abelsch falls die Verknüpfung kommutativ ist, d.h.
   $$\forall f,g \in G: fg=gf$$

5. Die Anzahl der Elemente von $G$ heißt von $G$ , geschrieben $\vert G\vert$

Sei $(G,\circ)$ eine Gruppe (Halbgruppe, Monoid). Dann heißt eine Teilmennge $U \subseteq G$ Untergruppe (Unterhalbgruppe, Untermonoid), geschrieben $U \leq G$ , falls $(U,\circ)$ eine Gruppe (Halbgruppe, Monoid) ist.

Sei $M \subseteq G$ Teilmenge einer Gruppe $G$ , dann heißt

$$\langle M \rangle:=\bigcap_{M\leq U \leq G}U$$

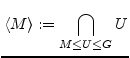
die von M erzeugte Gruppe. G heißt zyklische Gruppe , wenn

$$\exists g \in G:\langle g \rangle=G$$

Sei $G$ eine Gruppe, $U \leq G$ Untergruppe....

Sei G eine Gruppe, $U \leq G$ Untergruppe. Dann wird durch $f\sim g \Leftrightarrow fg^{-1}\in U$ eine $\uparrow$ Äquivalenzrelation definiert, dessen $\uparrow$ Äquivalenzklassen Rechtsnebenklassen von U genannt werden, geschrieben $[g]=Ug=\{ug\vert u\in U\}$ . Ebenso wird durch $f\sim g \Leftrightarrow f^{-1}g\in U$ eine Äquivalenzrelation definiert, dessen Äquivalenzklassen Linksnebenklassen von U genannt werden, geschrieben $[g]=gU=\{gu\vert u\in U\}$ .

Die Menge aller Rechtsnebenklassen von $U$ wird mit $U\\ G$ bezeichnet, die Menge aller Linksnebenklassen von $U$ mit $G/U$ . Die Zahl $\vert G\\ U\vert=\vert G/U\vert$ heißt Index der Untergruppe $U \leq G$ , geschrieben $(G:U)$ .

Kürzungsregel: Es seien $U\leq V\leq G$ Untergruppen. Dann gilt:

$$(G:U)=(G:V)(V:U)$$

Satz von Lagrange: Sei $H\leq G$ . Dann gilt:

$$\vert G\vert=(G:H)\vert H\vert$$

Sei $G$ Gruppe, $g\in G$ . Dann heißt $o(g):=\vert\langle g\rangle\vert$ die von g.

Kleiner Fermat: Sei G eine endliche Gruppe. Dann gilt:

$$\forall g\in G: g^{\vert G\vert}=e$$

Eine Untergruppe $N\leq G$ heißt Normalteiler, falls:

$$\forall g \in G: gN=Ng$$

Man schreibt hierfür $N\unlhd G$ . Eine Gruppe heißt einfach, wenn sie nur die trivialen Normalteiler $E:=\{e\}$ und $G$ besitzt.

Sei G eine Gruppe, $N\unlhd G$ Normalteiler, $U \leq G$ Untergruppe. Dann gilt:

1. $N\unlhd NU=\langle N,U\rangle \leq G$
2. $\vert N\vert,\vert U\vert<\infty \Rightarrow \vert NU\vert=\frac{\vert N\vert\vert U\vert}{\vert N\cap U\vert}$

Sei $G$ eine Gruppe. Eine Äquivalenzrelation $\equiv$ auf $G$ heißt Kongruenzrelation, wenn

$$\forall f_{1}, f_{2}, g_{1},g_{2} \in G: f_{1}\equiv f_{2} \wedge g_{1}\equiv g_{2} \Rightarrow f_{1}g_{1}\equiv f_{2}g_{2}$$

Sei $\equiv$ eine Kongruenzrelation auf Gruppe $G$ . Dann ist die Menge der Äquivalenzklassen $\overline{G}:=G/\equiv$ wieder eine Gruppe, die sogenannte Faktorgruppe .

Sei G eine Gruppe.

1. Für $N\unlhd G$ ist $f\equiv g :\Leftrightarrow fg^{-1} \in N$ eine Kongruenzrelation.
2. Ist $\equiv$ eine Kongruenzrelation auf $G$ , so gilt $[e]\unlhd G$ .