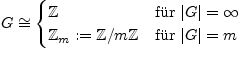Seien ![]() ,
, ![]() Gruppen. Eine Abbildung
Gruppen. Eine Abbildung
![]() heißt Gruppenhomomorphismus , falls
heißt Gruppenhomomorphismus , falls
. Falls
Homomorphisatz : Seien ![]() ,
, ![]() Halbgruppen,
Halbgruppen,
![]() ein Halbgruppenhomomorphismus. Dann gilt:
ein Halbgruppenhomomorphismus. Dann gilt:
Sind
Seien
![]() Gruppen und
Gruppen und
![]() Homomorphismen. Die Sequenz
Homomorphismen. Die Sequenz
heißt exaktk wenn
1. Isomorphisatz : Sei ![]() eine Gruppe,
eine Gruppe, ![]() ,
,
![]() . Dann gilt:
. Dann gilt:
2. Isomorphiesatz : Sei ![]() eine Gruppe,
eine Gruppe, ![]() .
Ferner sei
.
Ferner sei
. Dann gilt für ein
Sei
![]() . Dann existiert ein
. Dann existiert ein
![]() mit
mit
![]() .
.
Sei ![]() zyklische Gruppe. Dann gilt:
zyklische Gruppe. Dann gilt: